Artem Moskalev
Hi, I am Artem 👋. I am a Research Scientist at Johnson&Johnson, where I work on reimagining drug discovery with AI. My research focuses on geometric deep learning and language models, with a keen interest in developing geometry-aware methods that efficiently learn from unlabeled data.
Previously, I did my PhD at AMLab & VIS Lab at the University of Amsterdam, supervised by Prof. Arnold Smeulders and Prof. Erik Bekkers. My PhD focus was on geometric deep learning. I received MSc degree from Skolkovo Institute of Science and Technology, where I worked on high-dimensional convex optimization and inverse problems under the supervision of Prof. Anh-Huy Phan.
I love learning about cultures and history. I like folk and metal music. In my free time, I enjoy playing chess and padel.
Email | CV | LinkedIn | X | Bluesky | GitHub | Google Scholar

Selected publications
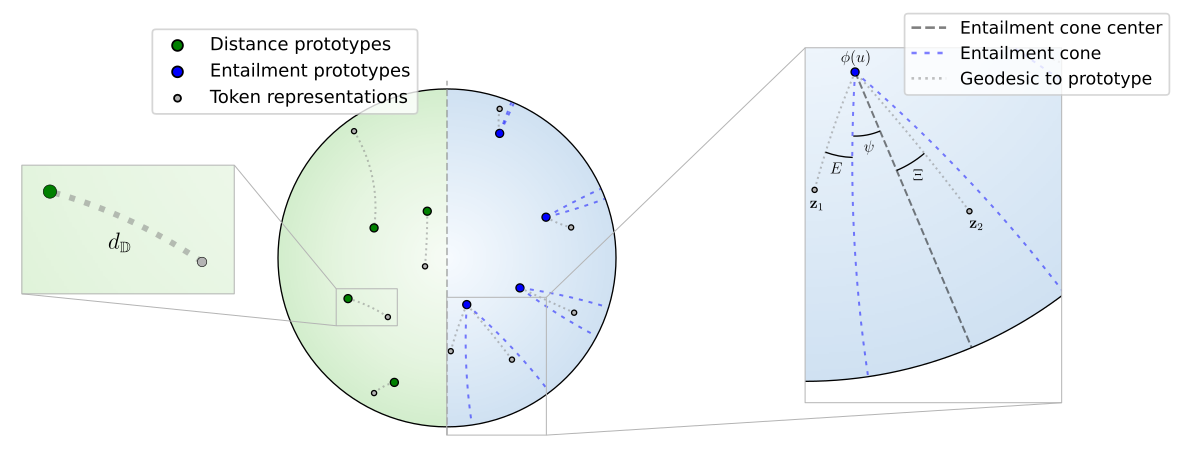
HyperHELM: Hyperbolic Hierarchy Encoding for mRNA Language Modeling
Preprint, 2025
We introduce HyperHELM, a framework that implements masked language model pre-training in hyperbolic space for mRNA sequences. Using a hybrid design with hyperbolic layers atop Euclidean backbone, HyperHELM aligns learned representations with the biological hierarchy defined by the relationship between mRNA and amino acids. Across multiple multi-species datasets, it outperforms Euclidean baselines and excels in out-of-distribution generalization.
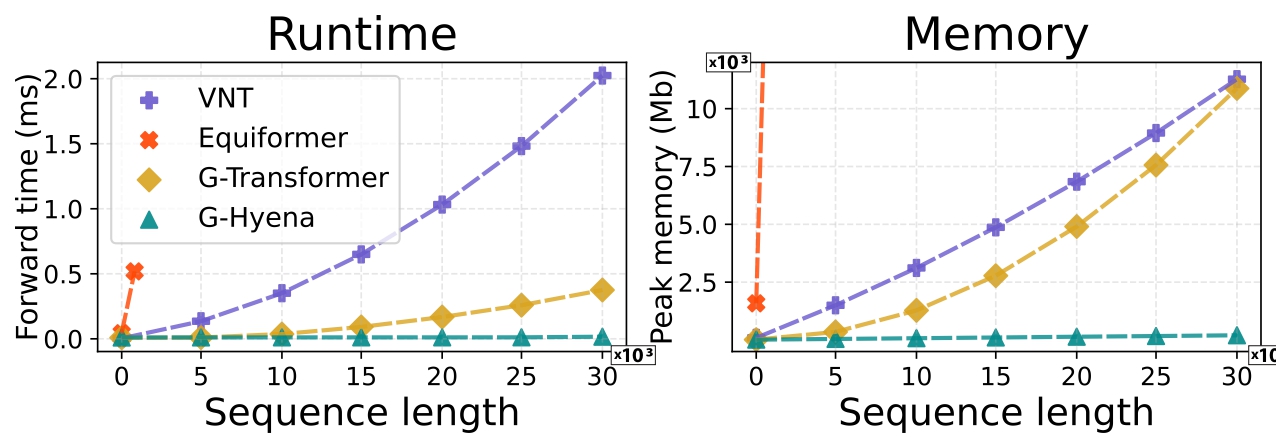
Geometric Hyena Networks for Large-scale Equivariant Learning
ICML, Spotlight, 2025
We introduce Geometric Hyena, the first equivariant long-convolutional model, combining sub-quadratic complexity with roto-translational equivariance. On large-scale RNA property prediction and protein dynamics, it outperforms prior models while using far less memory and compute, processing 30k tokens 20× faster and enabling 72× longer context than equivariant transformers at the same memory budget.
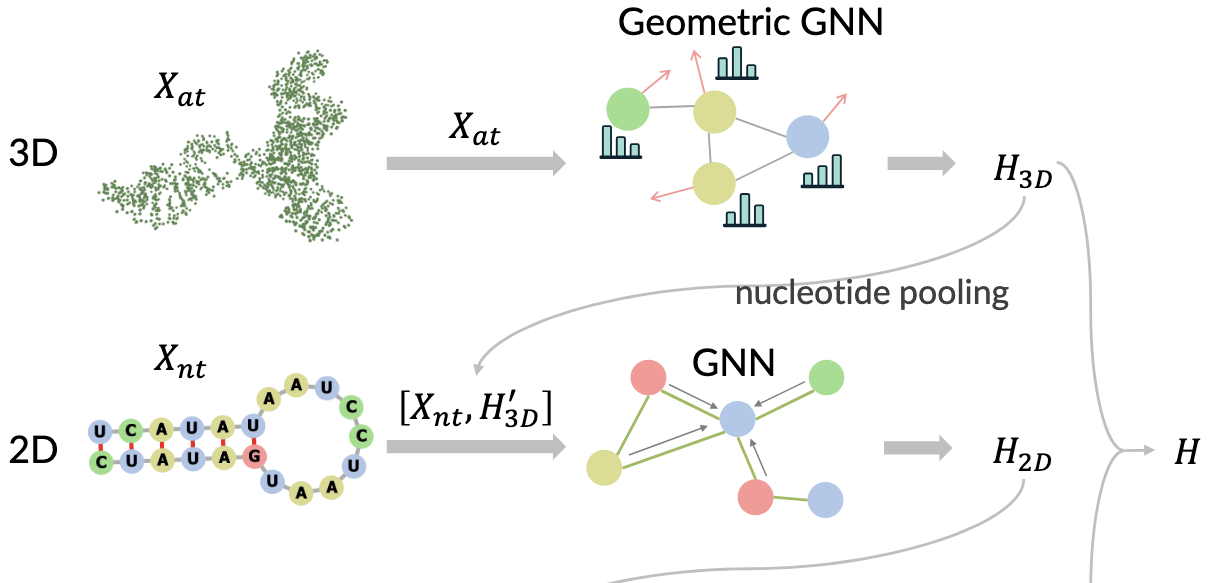
HARMONY: A Multi-Representation Framework for RNA Property Prediction
ICLR: AI for Nucleic Acids, Oral, 2025
We introduce HARMONY, a neural network that dynamically integrates 1D, 2D, and 3D representations, and seamlessly adapts to diverse real-world scenarios. Our experiments demonstrate that HARMONY consistently outperforms existing baselines across multiple RNA property prediction tasks on established benchmarks, offering a robust and generalizable approach to RNA modeling.
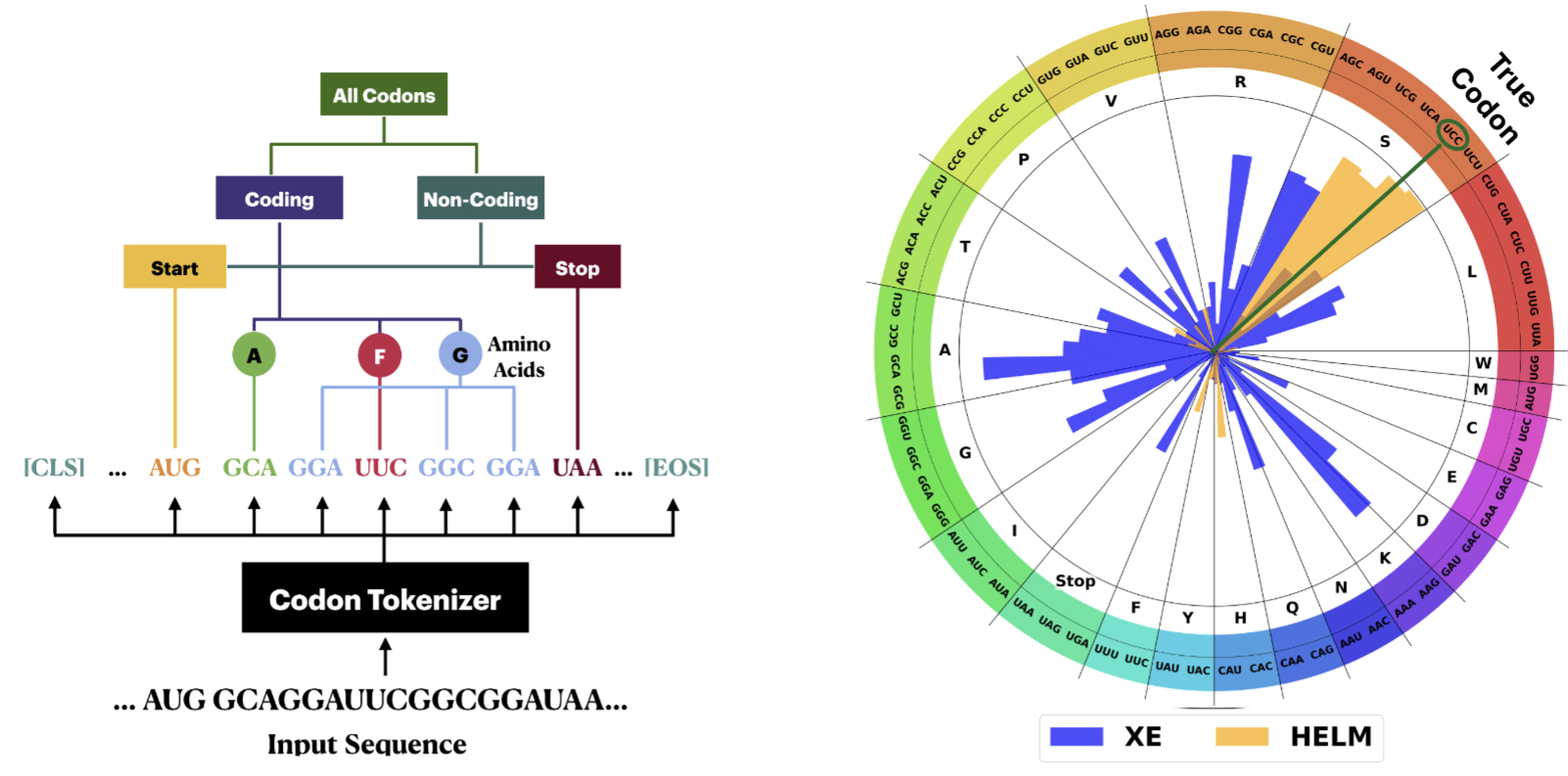
HELM: Hierarchical Encoding for mRNA Language Modeling
ICLR, 2025
We introduce Hierarchical Encoding for mRNA Language Modeling (HELM), a novel pre-training strategy that incorporates codon-level hierarchical structure into language model training. HELM modulates the loss function based on codon synonymity, aligning the model's learning process with the biological reality of mRNA sequences.
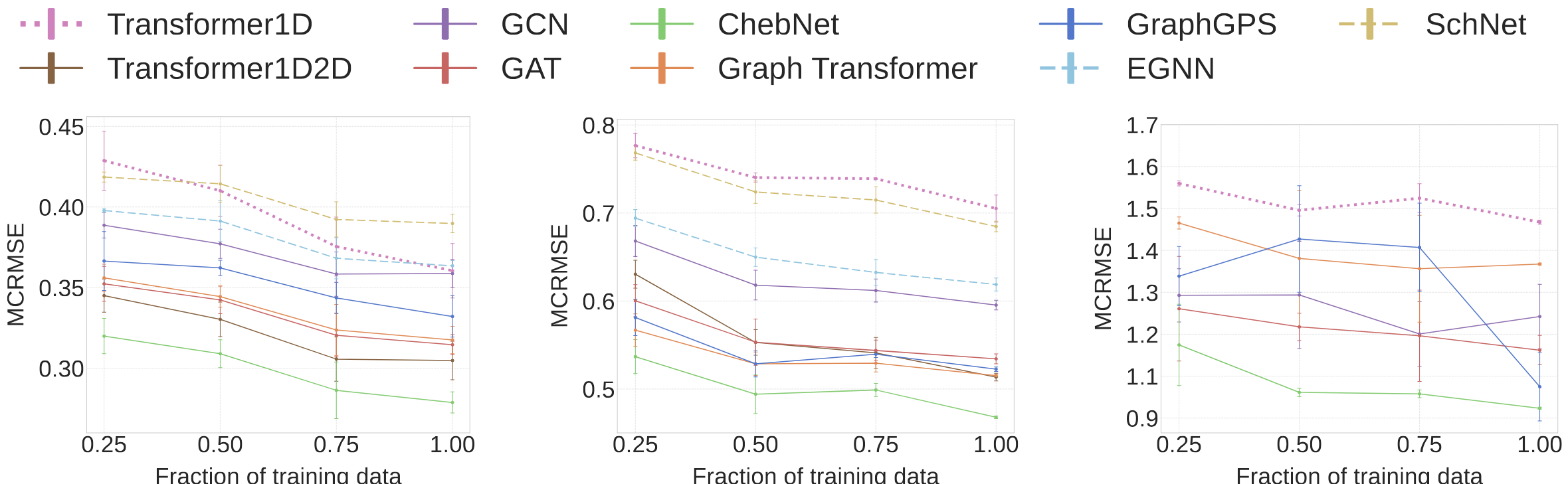
Beyond Sequence: Impact of Geometric Context for RNA Property Prediction
ICLR, 2025
We present the first systematic study of incorporating geometric context—beyond 1D sequences—into RNA property prediction. We reveal that geometry-aware models are more accurate while requiring less training data. At the same time, plain sequence-based models are the most robust to sequencing noise.
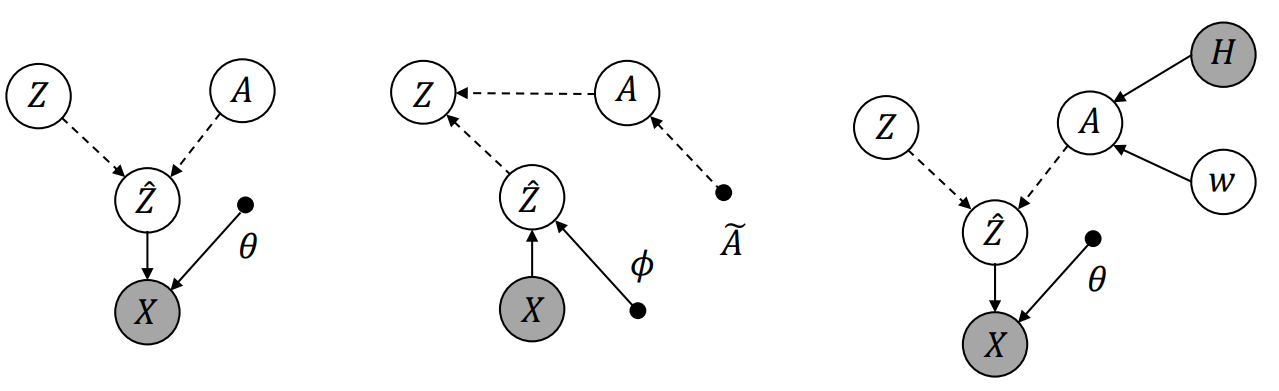
InfoSEM: A Deep Generative Model with Informative Priors for Gene Regulatory Network Inference
ICML, 2025
We present InfoSEM, an unsupervised model for GRN inference that uses pretrained gene embeddings and known interactions as priors. Unlike supervised methods that often exploit dataset-specific biases, InfoSEM captures true biological signals and achieves state-of-the-art performance on a biologically grounded benchmarks.
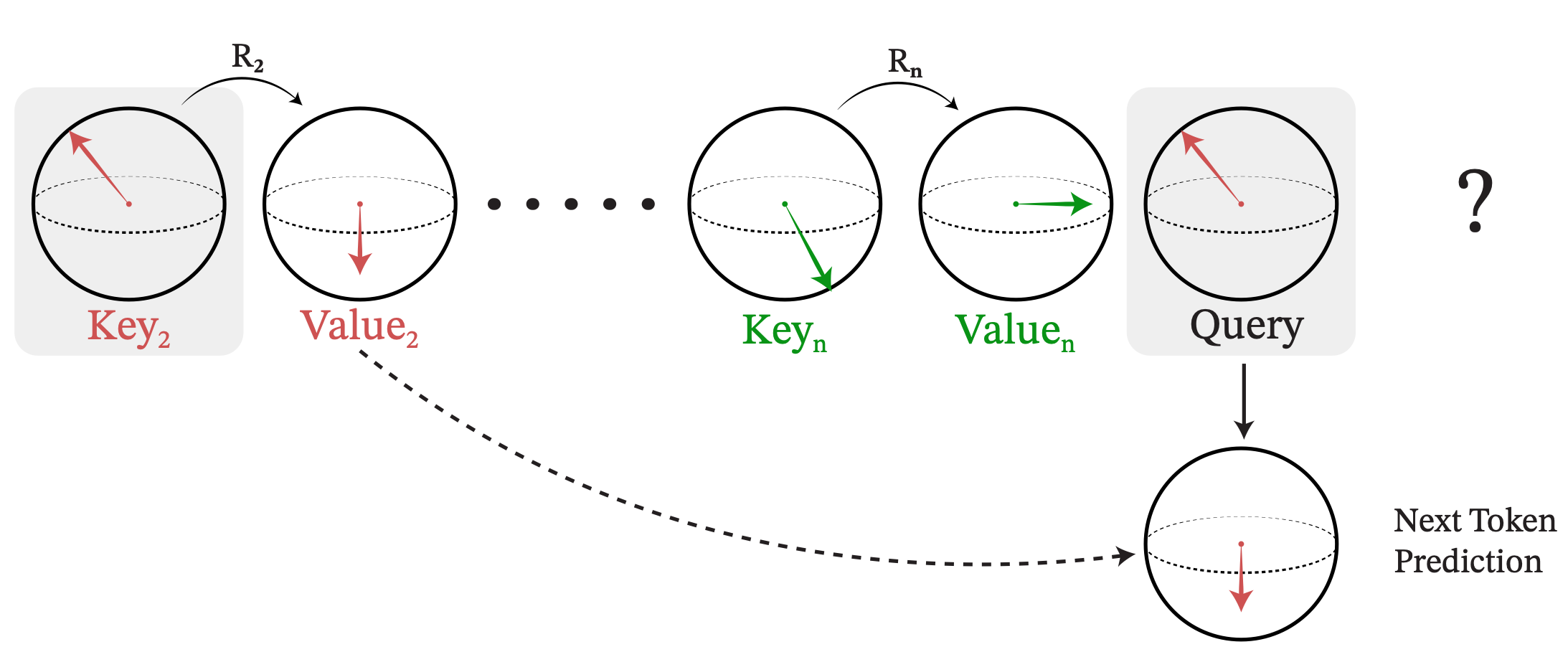
SE(3)-Hyena Operator for Scalable Equivariant Learning (Best Paper Award!!!)
ICML: Geometry-grounded Representation Learning and Generative Modeling, 2024
We introduce SE(3)-Hyena operator, a translation and rotation equivariant long-convolutional method to process global geometric context at scale with sub-quadratic complexity. Significantly more compute and memory efficient than transformers.
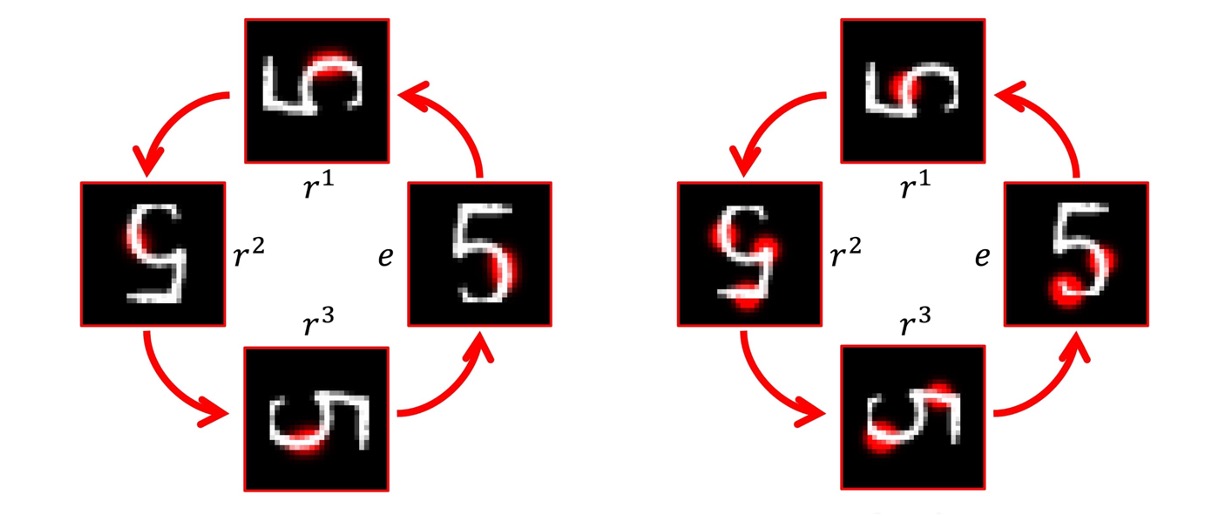
On genuine invariance learning without weight-tying
ICML: Topology, Algebra, and Geometry in Machine Learning, 2023
We study properties and limitations of invariance learned by neural networks from the data compared to the invariance achieved through equivariant weight-tying. We next address the problem of aligning data-driven invariance learning to the genuine invariance of weight-tying models.

LieGG: Studying Learned Lie Group Generators
NeurIPS, Spotlight, 2022
We present LieGG, a method to extract symmetries learned by neural networks and to evaluate the degree to which a network is invariant to these symmetries. With LieGG, one can explicitly retrieve learned invariances in a form of the generators of corresponding Lie-groups without any prior knowledge of the symmetries in the data.
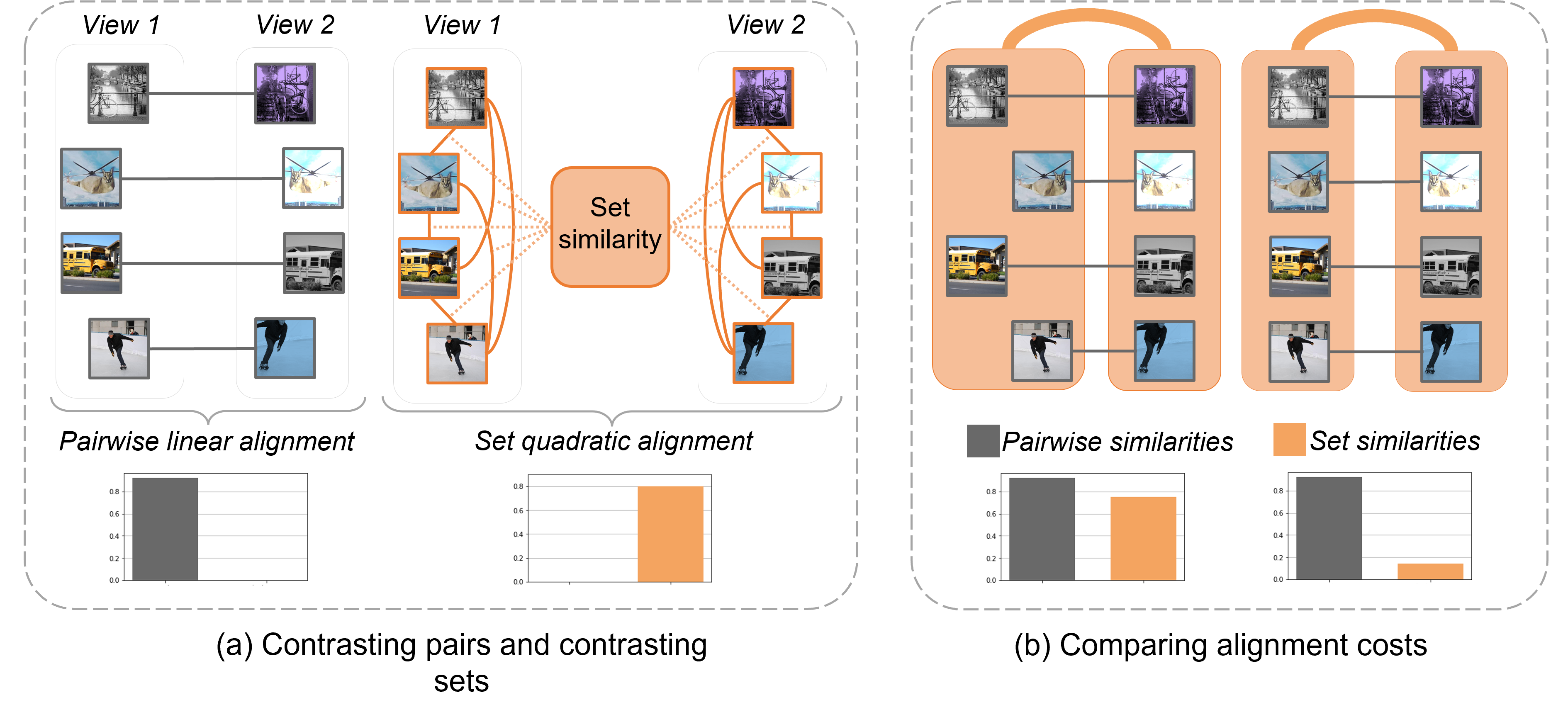
Contrasting quadratic assignments for set-based representation learning
ECCV, 2022
We go beyond contrasting individual pairs of objects by focusing on contrasting objects as sets. We use combinatorial quadratic assignment theory and derive set-contrastive objective as a regularizer for contrastive learning methods.
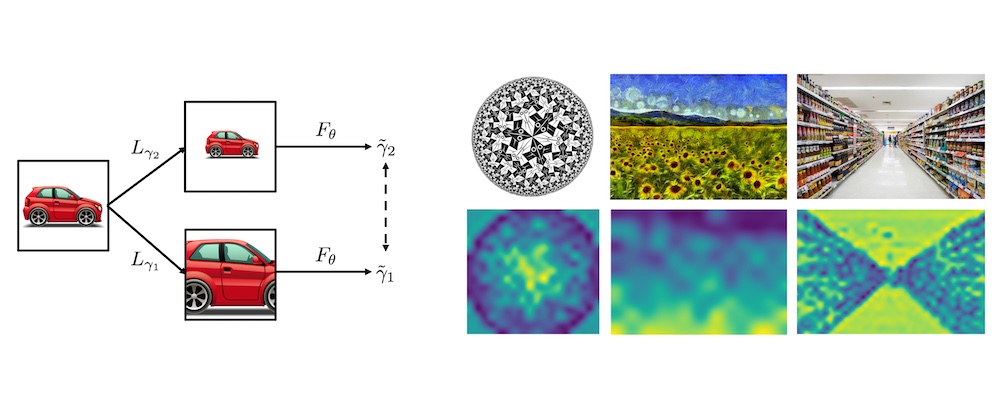
DISCO: accurate Discrete Scale Convolution (Best Paper Award!!!)
BMVC, Oral, 2021
We develop a better class of discrete scale equivariant CNNs, which are more accurate and faster than all previous methods. As a result of accurate scale analysis, they allow for a biased scene geometry estimation almost for free.
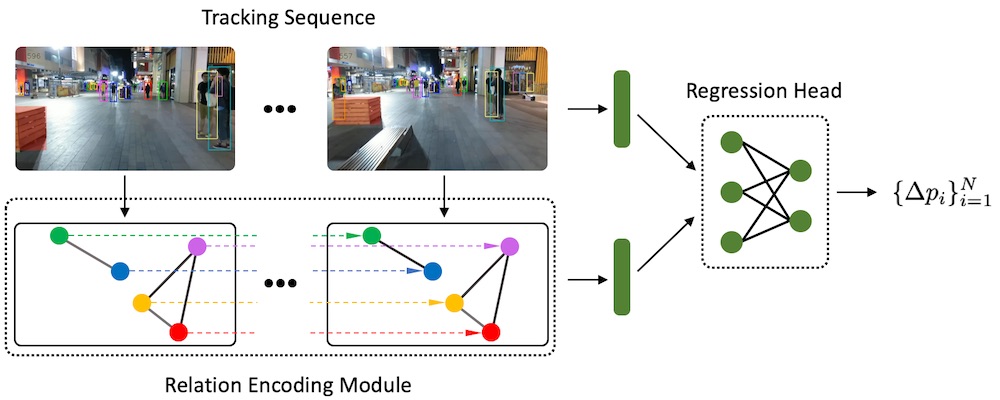
Relational Prior for Multi-Object Tracking
ICCV: VIPriors, Oral, 2021
Tracking multiple objects individually differs from tracking groups of related objects. We propose a plug-in Relation Encoding Module which encodes relations between tracked objects to improve multi-object tracking.

Scale Equivariance Improves Siamese Tracking
WACV, 2021
In this paper, we develop the theory for scale-equivariant Siamese trackers. We also provide a simple recipe for how to make a wide range of existing trackers scale-equivariant to capture the natural variations of the target a priori.
Highlights
- 🌟Happy to share that our Geometric Hyena has been selectet as a SPOTLIGHT at ICML2025.
- 🌟Our paper HARMONY on multi-representational learning for mRNA has been selected as ORAL on AI4NA@ICLR2025.
- We presented HELM: mRNA languge model at MILA Valence Multiomics reading group [video].
- We presented our paper on Impact of Geometric Context for RNA Property Prediction at MILA Valence Multiomics reading group [video].
- Our HELM paper on hierarchical language models for RNA is accepted to ICLR2025.
- Our Beyond Sequence paper on RNA modeling is accepted to ICLR2025.
- 🌟Our SE3-Hyena operator work has been awarded with outstanding paper award at GRaM@ICML!
- Our paper on scalable equivariant learning has been accepted to GRaM@ICML.
- I joined Janssen R&D at Johnson & Johnson as a Research Scientist.
- I successfully defended my doctoral thesis.
- Our paper on data-driven invariance learning will be presented in TAG-ML@ICML.
- I gave a talk on extracting learned symmetries at Geometric Deep Learning Seminar [video].
- Our paper on Lie group symmetry learning is accepted to NeurIPS2022 as SPOTLIGHT.
- I am attending International Gran Canaria School on Deep Learning.
- Our paper on set-based representation learning is accepted to ECCV2022.
- 🌟Our paper "DISCO: accurate Discrete Scale Convolution" has won BMVC 2021 Best Paper Award.
- Ivan Sosnovik and I gave a talk on "Scale-Equivariant CNNs for Computer Vision" at Computer Vision Talks [video].
Interns and Students
- Max van Spengler: Hyperbolic Hierarchy Encoding for mRNA Language Modeling
- Mehdi Yazdani-Jahromi: HELM - Hierarchical Encoding for mRNA Language Modeling
- Junjie Xu: Beyond Sequence - Impact of Geometric Context for RNA Property Prediction
- Evgenia Ilia: Efficient Self-Supervised Learning for Real-world Tabular Data
- Harm Manders: Dense contrastive learning for microscopy cell segmentation
- Lotte Bottema: Deep sequence modeling for trajectory forecasting
- Nadia Isiboukaren: Space-Time-Slot correspondence as a contrastive random walk for video object segmentation
- Jorrit Ypenga: Domain-regularization for siamese object tracking
Teaching
- Statistics, Simulation and Optimization, University of Amsterdam, 2019 – 2022
- Introduction to Image Processing, Skolkovo Institute of Science and Technology, 2018
Reviewing
- ICLR 24/25/26, NeurIPS 22/23, ICML 21/22/23, CVPR 19/20, ICCV/ECCV 19/20